仮想通貨初学者のブログ

気が向いたら書きます。主にDefiに興味があります。

秘密鍵からウォレットアドレスを作ってみる

概念的に秘密鍵と公開鍵がどういうものかは分かったが、もう少し踏み込んで理解してみたい人向けに多少暗号学の話に踏み入りつつ、実際に鍵が生成される流れをpythonを用いて見てみます。

いくらか数学的な話も出てくるかもしれませんが、数学をほとんど覚えていない人でも最後まで読める事を目標とし、対象読者としては暗号学を学ぶ程ではないけど言葉的な説明よりももうちょっと知りたい人を想定しています。

言葉で説明しながらコードを交えて書いていますが私の記事は冗長になりがちなのでコードだけみてそこから手っ取り早く取り組みたい方は以下にgoogle colaboratoryのリンクを貼っておくのでそちらからご覧ください。

colab.research.google.com

ちなみにgoogle colabのタイトルにもある通りこのコードは『マスタリング・イーサリアム』の第四章の内容を元に作成しています。本記事では説明しませんが、チェックサム等についてもソースコードを書いているので気になった方はそちらも見てみてください(英語版であればGithubから無料で読めます)

github.com

マスタリング・イーサリアム ―スマートコントラクトとDAppの構築

マスタリング・イーサリアム ―スマートコントラクトとDAppの構築

Amazon

秘密鍵と公開鍵の関係(おさらい)

まず簡単にそれぞれの鍵の説明から。秘密鍵は256bitの無作為に選ばれた数字です。実際に目にするのは以下のような16進数の64文字の文字列でありmetamaskから自身のアドレスの秘密鍵を確認する事ができます。(metamask右上の三点マーク -> アカウントの詳細 -> 秘密鍵のエクスポート)

秘密鍵 = 0xf8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

※秘密鍵については誰にも確認されないように気を付けてください。以降でも秘密鍵についてよく言及しますが、取り扱いには十分注意してください。

頭に0xが付くのはその文字列が16進数である事を明記する為の物です。

次に公開鍵です。公開鍵は秘密鍵から生成されるものです。公開鍵に後処理を加えた物がイーサリアムアドレスです。文字数は16進数表記で40文字分です。 ブロックチェーン界隈では イーサリアムアドレス=公開鍵 のように扱われる事が多い気がしますが、公開鍵をちょっといじる事でイーサリアムアドレスに変わるという認識を持っておくといいと思います。

イーサリアムアドレス = 0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9

トランザクションを作る際には自身の秘密鍵を用いて”署名”をする必要があります。逆に言えば秘密鍵さえあればトランザクションを作りそのウォレットから好き勝手に資産を移動させる事ができるという事です。（＝秘密鍵を知っているという事はそのアドレスの所有者とみなされる）よって秘密鍵を自分以外に誰も教えない事でそのウォレットの所有者が自分だけである事を主張できます。

ここで重要なのは秘密鍵から公開鍵を導く事は可能だが公開鍵から秘密鍵を求める事は困難であるという事です。ここら辺を深く立ち入ると大変難しい話になります。自分も正確には理解していませんが、最後に軽く説明します。

秘密鍵からイーサリアムアドレスの作り方

細かい話は置いておき、秘密鍵から公開鍵を経てイーサリアムアドレスを作る一連の流れを最初に説明してしまいます。

①秘密鍵を用意する(256bitの無作為な数字)

②楕円曲線方程式を満たすように秘密鍵から公開鍵を生成する

③公開鍵を連結してハッシュ化する

④ハッシュ化された公開鍵の最後の20バイト分を抜き出し頭に"0x"を付ける

①と④は分かりやすい作業です。ここでの壁は②で出てくる楕円曲線方程式です。③のハッシュ化に関しては今回は深く立ち入らずコードの方でもpysha3というライブラリを利用しています。気になる方は沢山記事があるのでググってみてください。

楕円曲線暗号

ここが本記事の山場です。より詳しい話は以下の参考記事・動画に任せるとして、ここでは(かなり)かみ砕いて話していこうと思います。

参考記事・動画

www.youtube.com

ja.wikipedia.org

まず楕円曲線について。楕円のイメージとは違うかもしれませんが一般的な楕円曲線は以下のように形をしています。

楕円曲線

そしてこの楕円曲線に対して足し算を定義します。ここがかなり混乱ポイントだと思います。ここでは通常の1+1=2のように用いる足し算とは異なる”通常の足し算に性質が似ている全く別の足し算”を新しく作ったと考えてください。

その新しい足し算ですが,書き方は通常の足し算と同じように以下のように書きます。

P + Q = R

ここでP,Q,Rは全て楕円曲線上の点を示しています。つまりそれぞれに入るのは(1, 10)や(-5, 7)のような座標です。単純な数字ではありません。新しく定義される足し算は座標と座標を使って新しい座標を求めるものです。では座標同士をどう足すのか？手順は二つあります。

①楕円曲線上の点Pと点Qにおいてその二点を結び楕円曲線上の線と交わった点を点R'とする。

②点R'をx軸に対して反転させた点を点Rとする。

・・・意味がよく分からないですね。図を用いて説明します。 （手書きですいません。）

加算の定義

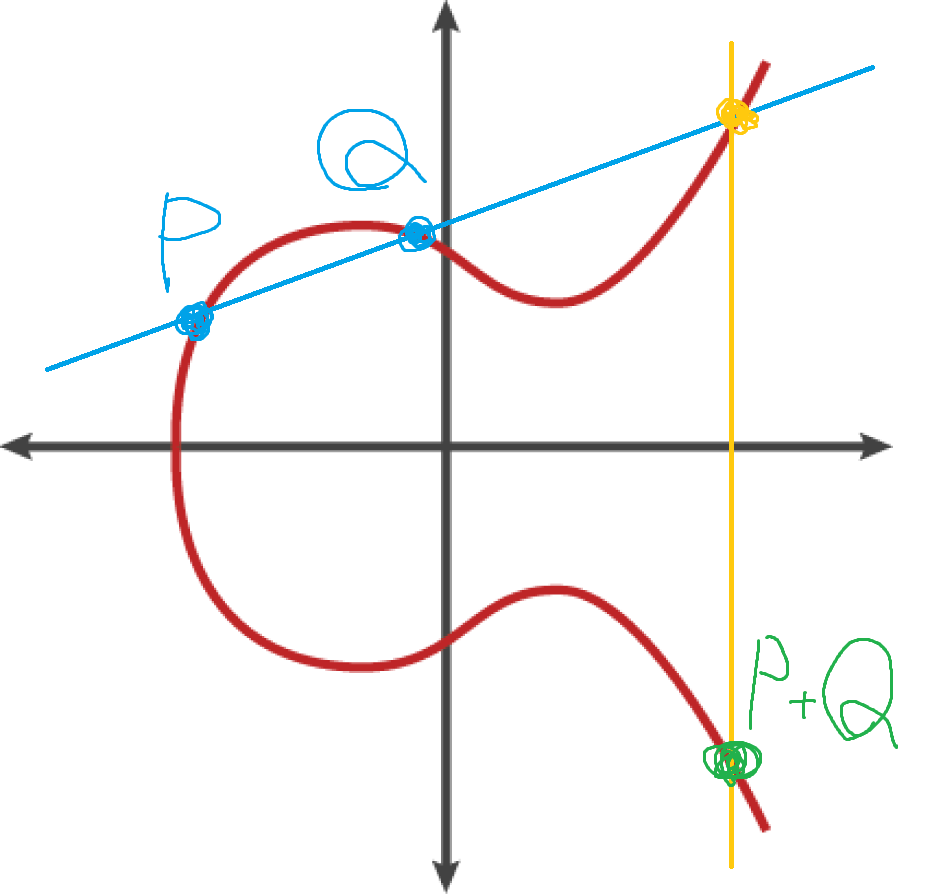
青線が楕円曲線上にある点Pと点Qを繋げた線です。この青線と楕円曲線が交わるポイントを点R'と呼んでいます。そしてx軸に対して反転した点、つまり点R'から垂線と楕円曲線の交点を点Rとします。(図ではP+Qと書いています)

これが新しい足し算の定義です。頭がこんがらがるかもしれませんが、落ち着いて何度か読み直してみてください。

そして秘密鍵から公開鍵の計算はこの楕円曲線上の足し算を用いて計算する事ができます。 先に式だけ書きます。まだ理解できなくて問題ありません。

K = k * G

ここでKが公開鍵, kが秘密鍵, Gが生成点と呼ばれる座標です。生成点は決まった定数を利用します。具体的には以下のような値です。とても大きな値です。

G = (Gx, Gy)

Gx = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798

Gy = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8

まず注意すべき事はK, Gは座標であり、kは単純な数字である事です。(秘密鍵kは256bitのランダムな数字列)

k(数字) * G(座標)の*は掛け算の意味で利用されており、G+G+G+...とGをk回足す事を意味します。もちろんここでの足すは楕円曲線上の足し算です。

つまりこの式の意味するところは

Gというあらかじめ決められた楕円曲線上の点から始めてG+G=2G, 2G+G=3G, 3G+G=4Gとk回繰り返し足し算を行っているという事です。 図にすると以下のようになります。まず初めにG+Gで2Gの点を求めて、その後にG+2Gで3Gの点を求めています。G+Gのように同じ値を足す場合の線は楕円曲線の接線を通るように引けば良いです。

公開鍵の求め方

足し算をするのにいちいち作図していたら大変ですが、実はこの足し算を計算で求める事ができる公式があります。 足し算の公式は以下です。流し見程度で良いと思います。(私も理解していません)

P(x_{1}, y_{1}) + Q(x_{2}, y_{2}) = R(x_{3}, y_{3})の求め方

x_{3} =\phi^{2}-x_{1}-x_{2}

y_{3} =-\phi x_{3}-\psi

\phi =\frac{y_{2}-y_{1}}{x_{2}-x_{1}}

\psi =\frac{y_{1} x_{2}-y_{2} x_{1}}{x_{2}-x_{1}}

さてこの公式によりわざわざ作図する手間が省けたという事でpythonのコードに落とし込んでいきます。

def add(p1, p2):
  x1 = p1[0]
  y1 = p1[1]
  x2 = p2[0]
  y2 = p2[1]

  # phi psiの計算はここではフェルマーの小定理を使っている
  phi = ((y2 - y1) * pow(x2 - x1, p-2, p)) % p
  psi = ((y1*x2 - y2*x1) * pow(x2 - x1, p-2, p)) % p

  x = (phi*phi - x1 - x2) % p
  y = (-phi * x - psi) % p
  return (x, y)

※よく見るとadd関数の中にはpで割ったあまりを求める操作が入っています。これまで楕円曲線は連続値であるかのように話をしていましたが、実際にはpという大きな素数で割った余りのみを扱う空間上で鍵は生成されています。ただし、今回はそこの説明は省いています。最後に軽く触れようと思います。

ここでもう一度公開鍵と秘密鍵の関係について戻ってみます。

K = k*G

k*GはG+G+G+...とk回Gを足し合わせるという事でした(Gは事前に決められた座標です)。先ほど足し算の計算方法は分かったので後はこれをk回足し合わせる、つまり秘密鍵の値の回数だけ足し算をすれば公開鍵を求める事が出来ます。

・・・とここで困ったことが起こります。それは秘密鍵kの値がとんでもなくでかいという事です。秘密鍵は最大で2の256乗(10の76乗程度)あります。つまり足し算を膨大な回数行わないといけません。残念ながらこの回数の計算は現在の計算機では現実的な時間で解くことができません。ということで計算は工夫する必要があります。

そこで例として4*G = G+G+G+Gを考えてみます。この時単純に4回足すのではなく 2G+2Gと変形するとG+G=2Gの計算と2G+2G=4Gの計算の二回で4Gを求める事ができます。

16*Gの場合はどうなるかというとG+G=2G,2G+2G=4G,4G+4G=8G,8G+8G=16G の4回の計算でするだけで求める事ができます。これはつまりk回足し算は工夫するとlogk回程度に計算回数を抑える事ができる事を意味しています。 logについて忘れてしまった方は特に気にする必要はありませんが、この工夫を利用するとk回(10の76乗程度)の計算回数を約300回程度に抑え込む事が可能になります。とんでもない改善です。この回数であれば爆速で計算する事が可能です。

ちなみに P+P=2Pのように座標を2倍にする操作に関しても同様に公式があり以下のようにコードに落とし込めます

def double(p1):
  x = p1[0]
  y = p1[1]
  phi = (((3 * x*x) % p) * pow(2 * y, p-2, p)) % p
  psi = (((-3*x*x*x + 2*y*y) % p) * pow(2 * y, p-2, p)) % p

  x = (phi*phi - 2 * x) % p
  y = (- phi * x - psi) % p
  return (x, y)

足し算と二倍の公式についてはこちらを参照しています。

ja.wikipedia.org

さてこれで秘密鍵から公開鍵を求める準備は整いました。あとは先ほど計算の工夫をコードに落とし込むだけです

def create_public_key(k, G):
  # 秘密鍵k
  _k = k
  # 生成点G
  _G = G
  i = 0
  cal_list = []
  while True:
    i += 1
    _quo = _k // 2
    _rem = _k % 2
    # _kが2で割り切れない場合最後に足し合わせる
    if _rem:
      cal_list.append(_G)

    _G = double(_G)
    _G = (int(_G[0]), int(_G[1]))
    _k = _quo

    if _k == 1:
      cal_list.append(_G)
      break

  _p = cal_list[0]
  for q in cal_list[1:]:
    _p = add(_p, q)
  return _p

それでは秘密鍵からイーサリアムアドレスを作る方法を再度確認します

①秘密鍵を用意する(256bitの無作為な数字)

②楕円曲線方程式を満たすように秘密鍵から公開鍵を生成する

③公開鍵を連結してハッシュ化する

④ハッシュ化された公開鍵の最後の20バイト分を抜き出し頭に"0x"を付ける

ここで秘密鍵はマスタリングイーサリアムでも用いられている

0xf8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

を使用します。 この秘密鍵のイーサリアムアドレスは

0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9

のようなので本当にそうなるかを確認してみます。

今回③のハッシュ化はpysha3というライブラリを用いて計算してしまいます。

# 秘密鍵k
print('秘密鍵:', str(hex(k)), '\n')
# 秘密鍵: 0xf8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315 


# 秘密鍵kと生成点Gを用いて公開鍵を生成する(一番計算がめんどくさい所)
public_key = create_public_key(k, G)


# 公開鍵のx点とy点
print('公開鍵K(Kx, Ky)')
print('Kx:', hex(public_key[0]))
print('Ky:', hex(public_key[1]), '\n')
# 公開鍵K(Kx, Ky)
# Kx: 0x6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b
# Ky: 0x83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0


# 公開鍵を連結
K = hex(public_key[0])[2:] + hex(public_key[1])[2:]
print('連結した公開鍵', '\n', K, '\n')
# 連結した公開鍵  
# 6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0 


# ハッシュ化
hash_K = hash_hex(K)
print('ハッシュ', '\n', hash_K, '\n')
# ハッシュ 
#  2a5bc342ed616b5ba5732269001d3f1ef827552ae1114027bd3ecf1f086ba0f9 

# 最後の20バイトを抜き出して0xをつける
address = '0x' + hash_K[-40:]
print('イーサリアムアドレス', '\n', address)
# イーサリアムアドレス 
#  0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9

無事に秘密鍵からイーサリアムアドレスを求める事ができるようになりました！！ 自分のアドレスの秘密鍵で計算してみたりすると面白いかもしれませんが、漏洩に十分気を付けてください。

さて、ここまでで私たちは適当な64文字の数列を用意すればいろんなイーサリアムアドレスを生成できるようになりました。ここで0x1111111111111111111111111111111111111111111111111111111111111111という秘密鍵を用いてイーサリアムアドレスを求めて計算してみました。どうやら0x19e7e376e7c213b7e7e7e46cc70a5dd086daff2aのようです。

このイーサリアムアドレスをetherscanでみてみましょう。

https://etherscan.io/address/0x19e7e376e7c213b7e7e7e46cc70a5dd086daff2a

transaction履歴が結構あるのが確認できます笑　ふざけてイーサを入れている人がいるという事だと思います。最初に言いましたが、あるイーサリアムアドレスの秘密鍵を知っているということはつまりそのイーサリアムアドレスの所有者とみなされます。つまりこのウォレットはあなたの物として好きなように使えるという事です。仮に今このウォレットにイーサが入っているのであればこのウォレットをmetamaskに登録して自分の他のウォレットにイーサを送ることは簡単にできてしまいます。(metamaskの画面右上のアカウントアイコンをクリック->アカウントのインポート->秘密鍵を入力で任意の秘密鍵に対してアカウントをインポートする事ができます。) 上のようなあまりにも分かりやすい(ランダムな数字でない)秘密鍵を持つことはハックのリスクになります。その為秘密鍵は完全な無作為な値にする必要があるのです。

以上で秘密鍵から公開鍵を経てイーサリアムアドレスを求める話は終わりです。 最後にいくつか付録を付けておこうと思います。

付録

なぜ公開鍵から秘密鍵を求める事ができないのか

2つの鍵の関係は以下でした。

K=k*G

仮にk=9だとすると実際にこの計算を行う前に9*Gは本文中の工夫により 4G+4G+G=9Gと計算すればいい事が分かります。ただしこれは事前にkが分かっていない場合には適用できません。公開鍵Kが分かっているけど秘密鍵が分からない場合1G, 2G, 3G, 4Gとしらみつぶしに公開鍵と一致するかを確かめるしかないのです。秘密鍵kの値が小さければこの方法でも求められそうですが、実際にはとんでもなく大きな値なのでこれを求めるには超膨大な計算量がかかってしまい現実時間では解けないという事です。注意として、現代のコンピュータで現実時間で解けないというだけであり、仮に今のコンピュータと比較にならないくらい早い神コンピュータが存在していた場合現実時間で解けてしまうという可能性はあるという事です。 さらに踏み込んでそもそもなぜこの楕円曲線暗号を使う必要があるのか等は他の本や記事を参照ください。

楕円曲線暗号について

本記事ではグラフに滑らかにプロットできるような楕円曲線を例に話したが、実際にイーサリアムで使われるものはsecp256k1というパラメーターで定義された楕円曲線が用いられています。 en.bitcoin.it

少し触れましたが、pythonの足し算と2倍算を実装する際には素数pでのモジュラー計算があります。実装する際には負の値と分数の値のモジュラー計算の変換方法やフェルマーの小定理が必要になります。ここではそれぞれについて解説しませんが、ググれば各自記事が出ると思いますので実装についてより気になった方は参考にしてみてください。